Teorema di Nielsen-Schreier - Nielsen–Schreier theorem

Nella teoria dei gruppi , una branca della matematica, il teorema di Nielsen-Schreier afferma che ogni sottogruppo di un gruppo libero è esso stesso libero. Prende il nome da Jakob Nielsen e Otto Schreier .

Enunciato del teorema

Un gruppo libero può essere definito da una presentazione di gruppo costituita da un insieme di generatori senza relazioni. Cioè, ogni elemento è un prodotto di una qualche sequenza di generatori e dei loro inversi, ma questi elementi non obbediscono ad alcuna equazione se non a quelle che seguono banalmente da gg ⁻¹ = 1. Gli elementi di un gruppo libero possono essere descritti come tutte le possibili parole ridotte , quelle stringhe di generatori e i loro inversi in cui nessun generatore è adiacente al proprio inverso. Due parole ridotte possono essere moltiplicate concatenandole e quindi rimuovendo eventuali coppie generatore-inverso che risultano dalla concatenazione.

Il teorema di Nielsen-Schreier afferma che se H è un sottogruppo di un gruppo libero G , allora H è esso stesso isomorfo a un gruppo libero. Cioè, esiste un insieme S di elementi che generano H , senza relazioni non banali tra gli elementi di S .

La formula di Nielsen–Schreier , o formula dell'indice di Schreier , quantifica il risultato nel caso in cui il sottogruppo abbia indice finito: se G è un gruppo libero di rango n (libero su n generatori), e H è un sottogruppo di indice finito [ G  : H ] = e , allora H è libero da rango . ${\displaystyle 1+e(n{-}1)}$

Esempio

Sia G il gruppo libero con due generatori , e sia H il sottogruppo costituito da tutte le parole ridotte di lunghezza pari (prodotti di un numero pari di lettere ). Allora H è generato dai suoi sei elementi Una fattorizzazione di qualsiasi parola ridotta in H in questi generatori e i loro inversi può essere costruita semplicemente prendendo coppie consecutive di lettere nella parola ridotta. Tuttavia, questa non è una presentazione libera di H perché gli ultimi tre generatori possono essere scritti nei termini dei primi tre come . Piuttosto, H è generato come un gruppo libero dai tre elementi che non hanno relazioni tra loro; o invece da parecchie altre triple dei sei generatori. Inoltre, G è libero su n = 2 generatori, H ha indice e = [ G  : H ] = 2 in G , e H è libero su 1 + e ( n –1) = 3 generatori. Il teorema di Nielsen-Schreier afferma che come H , ogni sottogruppo di un gruppo libero può essere generato come un gruppo libero, e se l'indice di H è finito, il suo rango è dato dalla formula dell'indice. ${\displaystyle a,b}$${\displaystyle a,b,a^{-1},b^{-1}}$${\displaystyle p=aa,\ q=ab,\ r=ba,\ s=bb,\ t=ab^{-1},\ u=a^{-1}b.}$${\displaystyle s=rp^{-1}q,\ t=pr^{-1},\ u=p^{-1}q}$${\displaystyle p=aa,\q=ab,\r=ba,}$

Prova

Il gruppo libero G = π ₁ ( X ) ha n = 2 generatori corrispondenti ai loop a , b dal punto base P in X . Il sottogruppo H di parole pari lunghezza, con indice e = [ G  : H ] = 2, corrisponde al grafico che copre Y con due vertici corrispondenti ai cosets H e H' = aH = bH = un ^-1 H = b ^{- 1} H , e due bordi sollevati per ciascuno dei bordi del loop originali a , b . Contraendo uno degli spigoli di Y si ottiene un'equivalenza di omotopia a un mazzo di tre cerchi, così che H = π ₁ ( Y ) è un gruppo libero su tre generatori, ad esempio aa , ab , ba .

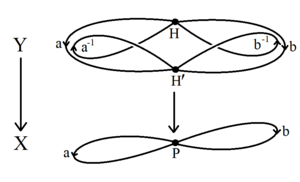
Una breve dimostrazione del teorema di Nielsen-Schreier usa la topologia algebrica dei gruppi fondamentali e degli spazi coprenti . Un gruppo libero G su un insieme di generatori è il gruppo fondamentale di un bouquet di cerchi , un grafo topologico X con un solo vertice e con un arco-arco per ogni generatore. Qualsiasi sottogruppo H del gruppo fondamentale è esso stesso il gruppo fondamentale di uno spazio coprente connesso Y → X. Lo spazio Y è un grafo topologico (possibilmente infinito), il grafo coset di Schreier ha un vertice per ogni coset in G/H . In qualsiasi grafo topologico connesso, è possibile restringere i bordi di un albero ricoprente del grafo, producendo un bouquet di cerchi che ha lo stesso gruppo fondamentale H . Poiché H è il gruppo fondamentale di un mazzo di cerchi, è esso stesso libero.

L'omologia semplice permette di calcolare il rango di H , che è uguale a h ₁ ( Y ), il primo numero di Betti dello spazio coprente, il numero di cicli indipendenti. Per G privo di rango n , il grafo X ha n archi e 1 vertice; supponendo che H abbia indice finito [ G  : H ] = e , il grafo di copertura Y ha en archi ed e vertici. Il primo numero di Betti di un grafo è uguale al numero di archi, meno il numero di vertici, più il numero di componenti connesse; quindi il rango di H è:

${\displaystyle h_{1}(Y)\,=\,en-e+1\,=\,1+e(n{-}1).}$

Questa prova si deve a Reinhold Baer e Friedrich Levi  ( 1936 ); la dimostrazione originale di Schreier forma il grafo di Schreier in modo diverso come quoziente del grafo di Cayley di G modulo l'azione di H .

Secondo il lemma del sottogruppo di Schreier , un insieme di generatori per una presentazione libera di H può essere costruito da cicli nel grafo di copertura formato concatenando un percorso di albero ricoprente da un punto base (il coset dell'identità) a uno dei coset, un singolo bordo non ad albero e un percorso ad albero ricoprente inverso dall'altro punto finale del bordo al punto base.

Fondamenti assiomatici

Sebbene siano note diverse dimostrazioni del teorema di Nielsen-Schreier, dipendono tutte dall'assioma della scelta . Nella dimostrazione basata su gruppi fondamentali di bouquet, per esempio, l'assioma della scelta appare sotto forma di affermazione che ogni grafo connesso ha un albero ricoprente. L'uso di questo assioma è necessario, poiché esistono modelli della teoria degli insiemi di Zermelo-Fraenkel in cui l'assioma della scelta e il teorema di Nielsen-Schreier sono entrambi falsi. Il teorema di Nielsen-Schreier a sua volta implica una versione più debole dell'assioma della scelta, per gli insiemi finiti.

Storia

Il teorema di Nielsen-Schreier è un analogo non abeliano di un risultato più antico di Richard Dedekind , secondo cui ogni sottogruppo di un gruppo abeliano libero è abeliano libero .

Jakob Nielsen ( 1921 ) originariamente dimostrò una forma ristretta del teorema, affermando che ogni sottogruppo finito di un gruppo libero è libero. La sua dimostrazione prevede l'esecuzione di una sequenza di trasformazioni di Nielsen sul gruppo elettrogeno del sottogruppo che ne riducono la lunghezza (come parole ridotte nel gruppo libero da cui sono tratte). Otto Schreier dimostrò il teorema di Nielsen-Schreier nella sua piena generalità nella sua tesi di abilitazione del 1926 , Die Untergruppen der freien Gruppe , anch'essa pubblicata nel 1927 in Abh. matematica. Sem. Amburgo. Univ.

La prova topologica basata su gruppi fondamentali di mazzi di cerchi è dovuta a Reinhold Baer e Friedrich Levi  ( 1936 ). Un'altra prova topologica, basata sulla teoria Bass-Serre delle azioni di gruppo sugli alberi , è stata pubblicata da Jean-Pierre Serre  ( 1970 ).

Guarda anche

• Teorema fondamentale dei gruppi ciclici , un risultato simile per i gruppi ciclici che nel caso infinito può essere visto come un caso speciale del teorema di Nielsen-Schreier

Appunti

Riferimenti

• Baer, ​​Reinhold ; Levi, Friedrich (1936), "Freie Produkte und ihre Untergruppen", Compositio Mathematica , 3 : 391-398.
• Fritto, Michael D. ; Jarden, Moshe (2008), Field arithmetic , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 11 (3a ed.), Springer-Verlag , p. 70, ISBN 978-3-540-77269-9, Zbl  1145.12001.
• Howard, Paul E. (1985), "Sottogruppi di un gruppo libero e l'assioma della scelta", The Journal of Symbolic Logic , 50 (2): 458–467, doi : 10.2307/2274234 , JSTOR  2274234 , MR  0793126.
• Johnson, DL (1980), Topics in the Theory of Group Presentations , serie di note di lezione della London Mathematical Society, 42 , Cambridge University Press, ISBN 978-0-521-23108-4.
• Johnson, DL (1997), Presentazioni di gruppi , testi per studenti della London Mathematical Society, 15 (2a ed.), Cambridge University Press, ISBN 978-0-521-58542-2.
• Läuchli, Hans (1962), "Auswahlaxiom in der Algebra", Commentarii Mathematici Helvetici , 37 : 1–18, doi : 10.1007/bf02566957 , hdl : 20.500.11850/131689 , MR  0143705 , S2CID  186223589.
• Magno, Guglielmo ; Karrass, Abramo; Solitar, Donald (1976), Teoria combinatoria dei gruppi (2a ed rivista), Dover Publications.
• Nielsen, Jakob (1921), "Om regning med ikke-kommutative faktorer og dens anvendelse i gruppeteorien", Math. Tidsskrift B (in danese), 1921 : 78–94, JFM  48.0123.03.
• Rotman, Joseph J. (1995), Introduzione alla teoria dei gruppi , Testi di laurea in matematica, 148 (4a ed.), Springer-Verlag, ISBN 978-0-387-94285-8.
• Serre, J.-P. (1970), Groupes Discretes , Extrait de l'Annuaire du College de France, Parigi.
• Serre, J.-P. (1980), Alberi , Springer-Verlag, ISBN 3-540-10103-9.
• Stillwell, John (1993), Classical Topology and Combinatorial Group Theory , Graduate Texts in Mathematics, 72 (2a ed.), Springer-Verlag.